其实这题的想法可以暴力一点的。。。

存在两个点之间有三条不相交的路径等价于存在两个环有边相交。这又等价于对于一颗生成树，存在一条树边同时被两条非树边覆盖。

用树上差分可以求出每条树边的覆盖次数进而进行判定，但是并没有必要，更主要的问题是树上差分虽然可以判断可行性，但难以给出一组方案。

直接暴力枚举非树边暴力覆盖，只要有一条树边的覆盖次数达到了 2 就可以退出了，因此只需要记每条树边被哪条非树边覆盖，如果覆盖 (a, b) 的时候发现有一条边已经被 (c, d) 覆盖了，那么根据 (a, b) 和 (c, d) 就可以得到方案。

不妨令 dfs 树作为生成树，令 b 为 a 的祖先，d 为 c 的祖先，b 的深度比 d 的深度浅。

不需要任何分类讨论，画个图就很容易明白，三条路径铁定就是：

• d -> lca(a, c)
• d -> b -> a -> lca(a, c)
• d -> c -> lca(a, c)

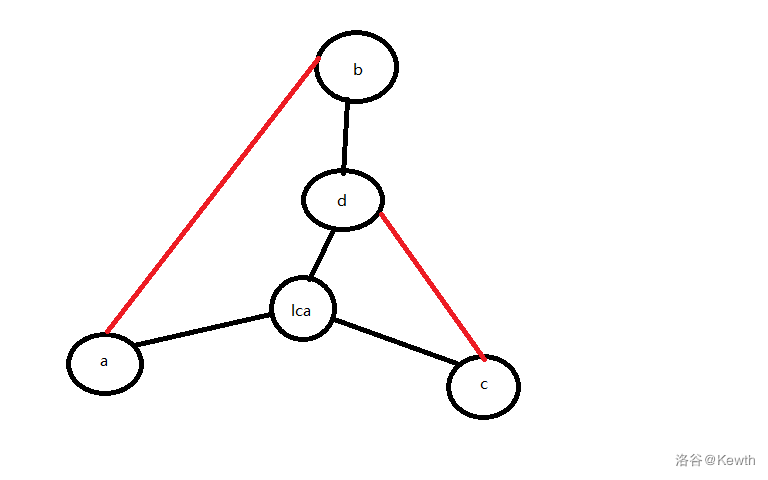
灵魂画手上线

求 lca 可以暴力求，路径也可以暴力找。

做法虽然暴力，复杂度却是线性的。

实现的时候可以一边 dfs 一边暴力覆盖，以下参考实现：

#include <cstdio>
#include <algorithm>
#include <vector>
#define debug(...) fprintf(stderr, __VA_ARGS__)

typedef long long ll;
struct {
    inline operator int () { int x; return scanf("%d", &x), x; }
    inline operator ll () { ll x; return scanf("%lld", &x), x; }
    inline operator char () { char x[3]; return scanf("%s", x), *x; }
} read;

const int maxn = 200005;
std::vector<int> G[maxn];
bool vis[maxn], ins[maxn];
int fa[maxn], deep[maxn];
int cx[maxn], cy[maxn];

int lca(int x, int y) {
    while(deep[x] > deep[y]) x = fa[x];
    while(deep[y] > deep[x]) y = fa[y];
    while(x != y) x = fa[x], y = fa[y];
    return x;
}

int tmp[maxn], tp;
void print() {
    printf("%d", tp);
    for(int i = 1; i <= tp; i ++)
        printf(" %d", tmp[i]);
    puts("");
    tp = 0;
}

void add_path(int x, int y) {
    while(x != y) {
        tmp[++ tp] = x;
        x = fa[x];
    }
    tmp[++ tp] = y;
}

void get(int a, int b, int c, int d) {
    if(deep[b] > deep[d]) {
        std::swap(a, c);
        std::swap(b, d);
    }
    int e = lca(a, c);

    puts("YES");

    add_path(e, d);
    std::reverse(tmp + 1, tmp + tp + 1);
    print();

    add_path(d, b);
    add_path(a, e);
    print();

    tmp[++ tp] = d;
    add_path(c, e);
    print();

    exit(0);
}

void dfs(int u) {
    deep[u] = deep[fa[u]] + 1;
    vis[u] = ins[u] = 1;
    for(int v : G[u])
        if(v != fa[u]) {
            if(!vis[v]) {
                fa[v] = u;
                dfs(v);
            }
            else if(ins[v]) {
                for(int x = u; x != v; x = fa[x])
                    if(cx[x] and cy[x])
                        get(cx[x], cy[x], u, v);
                    else {
                        cx[x] = u;
                        cy[x] = v;
                    }
            } 
        }
    ins[u] = 0;
}

int main() {
    int n = read, m = read;
    for(int i = 1; i <= m; i ++) {
        int u = read, v = read;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    for(int i = 1; i <= n; i ++)
        if(!vis[i])
            dfs(i);
    puts("NO");
}